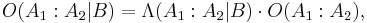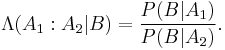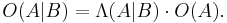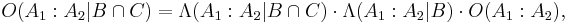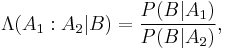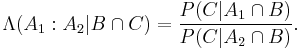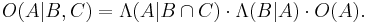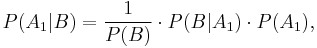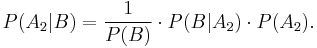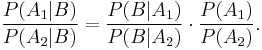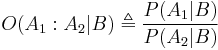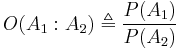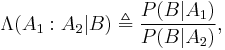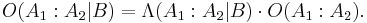Bayes' rule
In probability theory and applications, Bayes' rule relates the odds of event 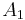 to event
to event 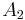 , before and after conditioning on event
, before and after conditioning on event  . The relationship is expressed in terms of the Bayes factor,
. The relationship is expressed in terms of the Bayes factor, 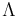 . Bayes' rule is derived from and closely related to Bayes' theorem. Bayes' rule may be preferred over Bayes' theorem when the relative probability (that is, the odds) of two events matters, but the individual probabilities do not. This is because in Bayes' rule,
. Bayes' rule is derived from and closely related to Bayes' theorem. Bayes' rule may be preferred over Bayes' theorem when the relative probability (that is, the odds) of two events matters, but the individual probabilities do not. This is because in Bayes' rule, 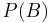 is eliminated and need not be calculated (see Derivation). It is commonly used in science and engineering, notably for model selection.
is eliminated and need not be calculated (see Derivation). It is commonly used in science and engineering, notably for model selection.
Under the frequentist interpretation of probability, Bayes' rule is a general relationship between 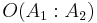 and
and 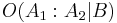 , for any events
, for any events 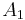 ,
, 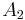 and
and  in the same event space. In this case,
in the same event space. In this case, 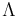 represents the impact of the conditioning on the odds.
represents the impact of the conditioning on the odds.
Under the Bayesian interpretation of probability, Bayes' rule relates the odds on probability models 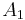 and
and 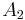 before and after evidence
before and after evidence  is observed. In this case,
is observed. In this case, 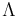 represents the impact of the evidence on the odds. This is a form of Bayesian inference - the quantity
represents the impact of the evidence on the odds. This is a form of Bayesian inference - the quantity 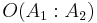 is called the prior odds, and
is called the prior odds, and 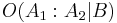 the posterior odds. By analogy to the prior and posterior probability terms in Bayes' theorem, Bayes' rule can be seen as Bayes' theorem in odds form. For more detail on the application of Bayes' rule under the Bayesian interpretation of probability, see Bayesian model selection.
the posterior odds. By analogy to the prior and posterior probability terms in Bayes' theorem, Bayes' rule can be seen as Bayes' theorem in odds form. For more detail on the application of Bayes' rule under the Bayesian interpretation of probability, see Bayesian model selection.
Contents |
The rule
Single event
Given events 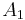 ,
, 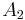 and
and  , Bayes' rule states that the conditional odds of
, Bayes' rule states that the conditional odds of  given
given  are equal to the marginal odds of
are equal to the marginal odds of  multiplied by the Bayes factor
multiplied by the Bayes factor 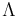 :
:
where
In the special case that 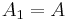 and
and 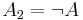 , this may be written as
, this may be written as
Multiple events
Bayes' rule may be conditioned on an arbitrary number of events. For two events  and
and  ,
,
where
In this special case, the equivalent notation is
Derivation
Consider two instances of Bayes' theorem:
Combining these gives
Now defining
this implies
A similar derivation applies for conditioning on multiple events, using the appropriate extension of Bayes' theorem
Examples
Frequentist example
Consider the drug testing example in the article on Bayes' theorem.
The same results may be obtained using Bayes' rule. The prior odds on an individual being a drug-user are 199 to 1 against, as 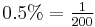 and
and 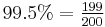 . The Bayes factor when an individual tests positive is
. The Bayes factor when an individual tests positive is 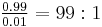 in favour of being a drug-user: this is the ratio of the probability of a drug-user testing positive, to the probability of a non-drug user testing positive. The posterior odds on being a drug user are therefore
in favour of being a drug-user: this is the ratio of the probability of a drug-user testing positive, to the probability of a non-drug user testing positive. The posterior odds on being a drug user are therefore 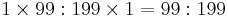 , which is very close to
, which is very close to 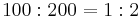 . In round numbers, only one in three of those testing positive are actually drug-users.
. In round numbers, only one in three of those testing positive are actually drug-users.
Model selection
External links
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay, discusses Bayesian model comparison in Chapters 3 and 28.